参考答案：[证] 由极限的保号性，存在δ＞0，当x∈[a-δ，a)时

，即得f(x)＜0．又因为

，所以存在x₀＜a-δ，当x≤x₀时，

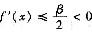．于是由微分中值定理得：
当x＜x₀，存在ξ∈(x，x₀)，使得

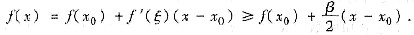
因此

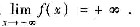
由

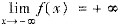，可知存在x₁＜a-δ，使得f(x₁)＞0，故对f(x)在区间[x₁，a-δ]上使用零点定理可得：f(x)在(x₁，a-δ)内至少有一个零点．从而f(x)在(-∞，a)内至少有一个零点．