阅读理解。
At a meeting, a well-known speaker lifted up a bill of 20 dollars before starting his speech.
Facing 200 people, he asked, "Who wants this 20-dollar bill?" A great many hands were put up. Then he
continued to say, "I intended to give it to any one of you, but allow me to do a thing before giving it to you."
Suddenly he crumpled (揉) it into a round mass. Then he asked, "Who wants it?" Still some hands were lifted
up.
He asked again, "Well, how could it be if I do it like this?" he threw the bill onto the ground, stepped on it
and twisted it. As he picked it up, the bill had become not only dirty but wrinkled.
"Who still wants it?" Still a few people put up their hands.
"My dear friends, you have had a meaningful class. No matter how I treated this bill, you still want it,
because it is worth 20 dollars. On your life road, you may be knocked down (击垮) or even broken into pieces
by your determination or unfavorable situations. We may feel ourselves worth nothing, but, my darling,
remember that whatever happens in the future, you should never lose your value (价值) in the God's heart.
You're particular-never forget it."
1. How many times did the speaker ask the people whether they wanted the bill? [ ]
A. Three times
B. Twice
C. Once
D. Four times
2. The underlined word "wrinkled" in the third paragraph probably means _____. [ ]
A. broken
B. flat
C. having small lines or folds in it
D. having holes in it
3. The speaker did this test in order to _____. [ ]
A. tell the audience that one should never lose one's own value
B. tell the audience that God values money most
C. test if some of the audience were extremely interested in money
D. play a trick on the audience
4. What would the speaker probably talk about next? [ ]
A. How money can make people crazy.
B. How to avoid being knocked down in one's life.
C. How to keep one's value of life.
D. How to give a meaningful class.
 成立.
成立.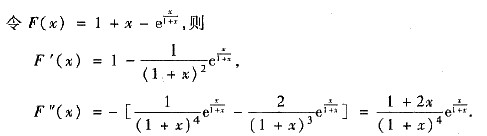
 在x>0时单调增加.又F’(0)=0,则当x>0时F’(x)
在x>0时单调增加.又F’(0)=0,则当x>0时F’(x)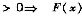 在x>0时单调增加.又因为F(0)=0,则当x>0时F(x)>0,即当x>0时,
在x>0时单调增加.又因为F(0)=0,则当x>0时F(x)>0,即当x>0时, <1+x成立.
<1+x成立.