问题
问答题
设函数f’(x)=x+acosx(a＞1)在区间(0，2π)内有极小值，且极小值为0，求函数在区间(0，2π)内的极大值．
答案
参考答案：f’(x)=1-asinx，令f’(x)=0，得
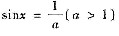，记
，可得区间(0，2π)内的驻点为x=x0，x=π-x0．
又f"(x)=-acosx，f"(x0)=-acosx0＜0，f"(π-x0)=acosx0＞0，则f(x)在x=x0处取得极大值，在x=π-x0处取得极小值．
由题设f(π-x0)=π-x0+acos(π-x0)=0，所以x0+acosx0=π，而f(x0)=x0+acosx0，故f(x)的极大值为π．