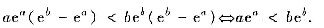参考答案：[证法一] 对函数f(x)=xe^x在区间[a，b]上使用拉格朗日中值定理可得

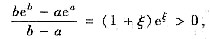
所以当b＞a＞0时，ae^a＜be^b，从而(a+b)e^a+b＜ae^2a+be^2b当b＞a＞0时成立．
[证法二] 令f(x)=xe^x，则f(x)=(x+1)e^x>0，即f(x)在x＞0时单调增加．故f(b)＞f(a)，
所以ae^a＜be^b，从而(a+b)e^a+b＜ae^2a+be^2b当b＞a＞0时成立．

解析： 不等式可改写为