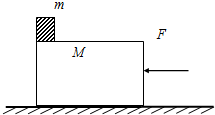
如图所示,在水平地面上有一个长L=1.5m,高h=0.8m的长方体木箱,其质量为M=1kg,与地面间的动摩擦因数μ=0.3.在它的上表面的左端放有一质量为m=4kg的小铁块,(铁块与木箱间的摩擦不计).开始它们均静止.现对木箱施加一水平向左的恒力F=27N.(g=10m/s2)求:
(1)经过多长时间铁块从木箱上滑落?
(2)铁块滑落前后木箱的加速度a1与a2大小之比.
(3)铁块着地时与木箱右端的水平距离S.
(1)对木箱进行受力分析,根据牛顿第二定律得:a1=F-μ(M+m)g M
代入数据得:a1=12m/s2
L=
a1t121 2
解得:t1=0.5s
(2)铁块滑落前后,对木箱进行受力分析,根据牛顿第二定律得:a2=F-μMg M
代入数据得:a2=24m/s2
∴
=a1 a2 1 2
(3)铁块离开木箱后做自由落体运动,则有:
h=
gt221 2
解得:t2=0.4s
铁块离开木箱时,木箱的速度为:v1=a1t1=6m/s
根据位移时刻公式得:
s=v1t2+
a2t221 2
解得:s=4.32m
答:(1)经过0.5s铁块从木箱上滑落;
(2)铁块滑落前后木箱的加速度a1与a2大小之比为1:2;
(3)铁块着地时与木箱右端的水平距离为4.32m.
