问题
问答题
设x∈[0，2]时，有|f(x)|≤1，|f"(x)|≤1，证明：对于x∈[0，2]，有|f’(x)|≤2．
答案
参考答案：[证] 对x∈[0，2]，将f(t)在x点展开为一阶泰勒公式
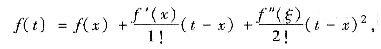
上式中令t分别取0，2得
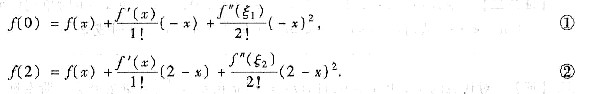
②-①可得
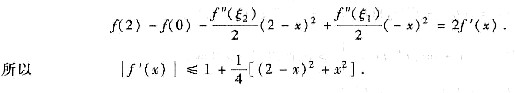
用“最值法”不难证明
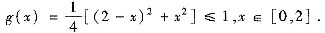所以对于x∈[0，2]，有|f’(x)|≤2．
搜题请搜索小程序“爱下问搜题”
设x∈[0，2]时，有|f(x)|≤1，|f"(x)|≤1，证明：对于x∈[0，2]，有|f’(x)|≤2．
参考答案：[证] 对x∈[0，2]，将f(t)在x点展开为一阶泰勒公式
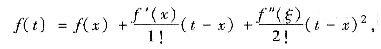
上式中令t分别取0，2得
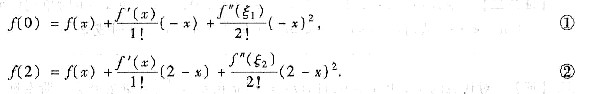
②-①可得
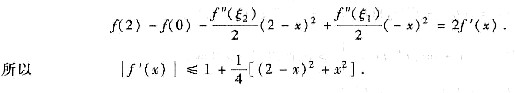
用“最值法”不难证明
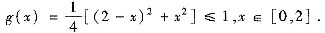所以对于x∈[0，2]，有|f’(x)|≤2．