下列命题
①设函数f(x)在(a,b)内可导,且f(a)=f(b),则至少有一点ξ∈(a,b),使f’(ξ)=0
②设函数f(x)在[a,b]上连续,在(a,b)内可导,且有一点ξ∈(a,b),使f’(ξ)=O,则必存在x1,ξ∈(a,b),使得f(x1)=f-(x2)
③设函数f(x)在(a,b)内可导,
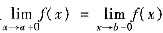 ,则至少有一点ξ∈(a,b),使f’(ξ)=0
,则至少有一点ξ∈(a,b),使f’(ξ)=0
④设函数f(x)在[a,+∞)上连续,在(a,+∞)内可导,且
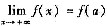 ,则至少有一点ξ∈(a,+∞),使f’(ξ)=0
,则至少有一点ξ∈(a,+∞),使f’(ξ)=0
中正确的是
(A) ①、③. (B) ①、④. (C) ②、③. (D) ③、④.
参考答案:D
解析: ①小正确.例如,函数
 在(0,1)内可导,且f(0)=f(1)=1,但对任意的ξ∈(0,1),f’(ξ)≠0.由此可知,罗尔定理中函数f(x)在[a,b]上连续的条件不可缺少.
在(0,1)内可导,且f(0)=f(1)=1,但对任意的ξ∈(0,1),f’(ξ)≠0.由此可知,罗尔定理中函数f(x)在[a,b]上连续的条件不可缺少.
[评注] 罗尔定理中函数三个条件缺一不可.例如函数f(x)=|x|,在[-1,1]上连续,且f(-1)=f(1),但在(-1,1)内不存在ξ,使_f’(ξ)=0成立.由此可知,罗尔定理中函数f(x)在(a,b)内可导的条件不可缺少.
又例如函数f(x)=x在[0,1]上连续,在(0,1)内可导,但对任意的ξ∈(0,1),f’(ξ)≠0.这说明罗尔定理中f(a)=f(b)的条件不可缺少.
②不正确.例如函数f(x)=x3,在[-1,1]上连续,在(-1,1)内可导,且f’(0)=0,但在区间[-1,1]上函数值处处都不相等.
③正确.请同学证明之.
④正确.设函数
 ,y∈[0,1),则f[g(y)]在[0,1)连续,在(0,1)内可导.定义函数
,y∈[0,1),则f[g(y)]在[0,1)连续,在(0,1)内可导.定义函数

则F(y)在[0,1]上连续,在(0,1)内可导,且F(0)=F(1)=f(a).根据罗尔定理知:至少存在一点η∈(0,1),使F’(η)=0,即

于是f[g(η)]=0.
取
 ,则f’(ξ)=f’[g(η)]=0.
,则f’(ξ)=f’[g(η)]=0.
综上分析,应选(D).
