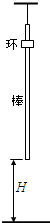
如图所示,一轻绳吊着粗细均匀的棒,棒下端离地面高H,上端套着一个细环.棒和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力kmg(k>1).断开轻绳,棒和环自由下落.假设棒足够长,与地面发生碰撞时,触地时间极短,无动能损失.棒在整个运动过程中始终保持竖直,空气阻力不计.求:
(1)棒第一次与地面碰撞弹起上升过程中,环的加速度;
(2)从断开轻绳到棒与地面第二次碰撞的瞬间,棒运动的路程S;
(3)从断开轻绳到棒和环都静止,摩擦力对环及棒做的总功W.
(1)设棒第一次上升过程中,环的加速度为a环,
由牛顿第二定律得:kmg-mg=ma环
解得:a环=(k-1)g,方向竖直向上
(2)设棒第一次落地的速度大小为v1
由机械能守恒得:
2m1 2
=2mgHv 21
解得:v1=2gH
设棒弹起后的加速度为a棒,由牛顿第二定律得:
a棒=-(k+1)g
棒第一次弹起的最大高度为:H1=v 21 2a棒
解得:H1=H k+1
棒运动的路程为:S=H+2H1=
Hk+3 k+1
(3)解法一:
棒第一次弹起经过t1时间,与环达到相同速度v′1
环的速度:v′1=-v1+a环t1
棒的速度:v′1=v1+a棒t1
环的位移:h环1=-v1t1+
a环1 2 t 21
棒的位移:h棒1=v1t1+
a棒1 2 t 21
环第一次相对棒的位移为:x1=h环1-h棒1=-2H k
棒环一起下落至地:
-v 22
=2gh棒1v /21
解得:v2=2gH k
同理,环第二次相对棒的位移为x2=h环2-h棒2=-2H k2
…xn=-2H kn
环相对棒的总位移为:x=x1+x2+…+xn
摩擦力对棒及环做的总功为:W=kmgx=-2kmgH k-1
解法二:
设环相对棒滑动距离为l
根据能量守恒 mgH+mg(H+l)=kmgl
摩擦力对棒及环做的总功为:W=-kmgl
解得:W=-
.2kmgH k-1
答:(1)环的加速度为(k-1)g,方向竖直向上.
(2)从断开轻绳到棒与地面第二次碰撞的瞬间,棒运动的路程:S=H+2H1=
H.k+3 k+1
(3)从断开轻绳到棒和环都静止,摩擦力对环及棒做的总功W=-
.2kmgH k-1
