下列结论正确的是
(A) 若函数f(x)在(a，b)内可导，则至少有一点ξ∈(a，b)，使
．
(B) 若函数f(x)在[a，b]上连续，在(a，b)内可导，则对任意的ξ∈(a，b)，必存在不同的x1，x2∈(a，b)，使f(x2)-f(x1)=f’(ξ)(x2-x1)成立．
(C) 设不恒为常数的函数f(x)在[a，b]上连续，在(a，b)内可导，且f(a)=f(b)，则在(a，b)内至少存在一点ξ，使f’(ξ)＞0．
(D) 在拉格朗日中值定理
(ξ介于x，a之间)中，ξ必定是x的连续函数．
参考答案：C
解析： 对于(A)：例如函数
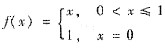，在(0，1)内可导，且f’(x)=1，x∈(0，1)，而
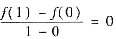．这说明拉格朗日巾值定理中，函数f(x)在[a，b]上连续的条件不可缺少．故(A)不正确．
[评注] 拉格朗日中值定理中函数f(x)在(a，b)内可导的条件也必不可少．例如函数f(x)=|x|在[-1，1]上连续，
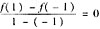．虽然f(x)在(-1．0)，(0，1)内可导，但不存在ξ∈(-1，1)，使f’(ξ)=0．这说明拉格朗日中值定理中，函数f(x)在(a，b)内可导的条件必不可少．
对于(B)：例如函数f(x)=x3在[-1，1]上连续，在(-1，1)内可导，取ξ=0，则f’(ξ)=0．而对[-1，1]内的任何两点x1＜x2都有
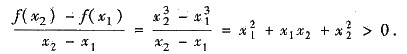
这说明拉格朗日中值定理中的条件是充分的，但不是必要的．故(B)不正确．
对于(D)：例如函数
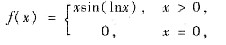
当x＞0时，
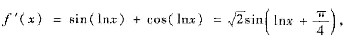
且有f(x)-f(0)=xf’(ξ)，
其中ξ=ξ(x)满足0＜ξ(x)＜x．以下应用反证法证明ξ=ξ(x)在任意小区间(0，ε)内都不连续．
设ξ=ξ(x)在(0，ε)内连续．
另一方面，当x→0时，ξ=ξ(x)→+0，所以总存在δ∈(0，ε)，使得ξ(δ)＜e-2Nπ+π/4=xN．因为ξ=ξ(x)在
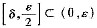内连续，所以根据介值定理知，存在
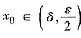，使得
ξ(x0)=e-2Nπ+π/4，于是f(x0)-f(0)=x0·f’[ξ(x0)]，即
故(D)也不正确．
由排除法可知(C)正确．应诜(C)．