Mainland couples who give birth to a second child in Hong Kong will be fined forbreaking the family planning policy a senior official has warned. As more women flock to Hong Kong to give birth to their second child,Zhang Feng,family planning department director of Guangdong Province,stressed that this violated Chinaspolicies. “And those who are government employees will even be dismissed from their posts.”he said.
''It doesn't matter if they give birth to their second child on the mainland or in other countries and regions, they have violated the country's policies and the province's regulations''.
He said that some families had been punished in the past few months after having a second child in Hong Kong, but gave no details.
Zhang made his remarks when a Hong Kong newspaper carried a controversial notice claiming residents' medical services had been affected by the growing number of mainland women who arrive in the city to give birth and gain right of abode (居住) there.
According to statistics revealed by Hong Kong Special Administrative Region government, about 88,000 babies were born in Hong Kong in 2010, but more than 41,000 or 47 percent, were to mainland couples, including a large number from Guangdong.
Hong Kong has limited the number of mainland women permitted to give birth in the city at 34,000 this year.
The issue also has caused calls for an amendment to Hong Kong's Basic Law so that babies born to mainland women are no longer granted permanent right of abode.
''I support Hong Kong government's decision to reduce or limit the number for mainland women giving birth in Hong Kong.'' Zhang said.
China introduced its family planning policy in 1979 to limit births in the world's most populous nation, although the rules have been relaxed in recent years.
小题1:Which of the following is true?
A.Zhang Feng is family planning department director of Guangdong Province.
B.Many government employees have been dismissed from their posts.
C.Those who give birth to a second child in Hong Kong will be fined.
D.It doesn’t matter if they give birth to their second child on the mainland.小题2: What does the word ''violated'' mean in the second paragraph?
A.was obeyed
B.went against
C.was for
D.was dismissed小题3:Zhang Feng said that______.
A.few families had been punished after having a second child in China
B.about 88,000 babies were born in Hong Kong in 2010
C.he agreed to reduce or limit the number for mainland women giving birth in Hong Kong
D.the residents' medical services in Hong Kong had been affected小题4:From the passage we can infer______.
A.in 2010 most of the babies born in Hong Kong belonged to mainland couples
B.babies born to mainland women in Hong Kong can't get permanent right of abode now
C.the number of mainland women permitted to give birth in Hong Kong has been reduced
D.the family planning policy in China is as strict as before小题5:Which is NOT the reason why some people want to give birth to a second child in Hong Kong?
A.They want to gain right of abode there for their babies.
B.They want to escape being punished for breaking the family planning policy.
C.They want their babies to enjoy the good medical services in Hong Kong.
D.They want to cause calls for an amendment to Hong Kong's Basic Law.
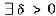 使得当a∈(a,a+δ)时f(x)-f(a)<0,因此,f(a)不是f(x)在[a,b]上的最小值.
使得当a∈(a,a+δ)时f(x)-f(a)<0,因此,f(a)不是f(x)在[a,b]上的最小值.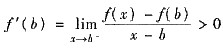 ,知
,知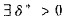 使得当x∈(b-δ*,b)时f(x)-f(b)<0,因此,f(b)也不是f(x)在[a,b]上的最小值.
使得当x∈(b-δ*,b)时f(x)-f(b)<0,因此,f(b)也不是f(x)在[a,b]上的最小值.