问题
问答题
设函数f(x)在(-∞，+∞)内可导，且满足
，证明：对任意实数。，存在ξ∈(-∞，+∞)，使得f’(ξ)=a．
答案
参考答案：[证] 对任意实数。，由
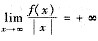知，
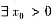，使当|x|＞x0时，有
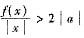，即f(x)>2|c|．令φ(x)=f(x)=ax，则由极限保号性可得
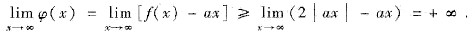
于是φ(x)在(-∞，+∞)内必有最小值，即存在ξ∈(-∞，+∞)，使得
，
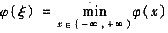显然φ(x)在(-∞，+∞)内可导，于是应有φ’(ξ)=0，即f’(ξ)=a．
解析： 由欲证不等式，可作辅助函数φ(x)=f(x)-ax，并证明limφ(x)=+∞，进而得知φ(x)在(-∞，+∞)内有最小值，最后由费马定理可得结论．