问题
单项选择题
下列命题中正确的是
(A) 设x0∈(a，b)，函数f’(x)满足f’(x)＞0(a＜x＜x0)和f’(x)＜0(x0＜x＜b0)，则f(x)在点x=x0处取得它在(a，b)上的最大值．
(B) 设f(x)在点x=x0处取得极大值，则存在正数δ＞0，使函数在(x0-δ，x0)中单调增加，在(x0，x0+δ)中单调减少．
(C) 设f(x)在区间(-a，a)内为偶函数(其中a为大于零的常数)，则x=0必是f(x)的一个极值点．
(D) 设f(x)在区间(-a，a)内可导且为偶函数(其中a为大于零的常数)，则f’(0)=0．
答案
参考答案：D
解析： 设f(x)在区间(-a，a)内可导且为偶函数，所以f’(x)在区间(-a，a)内为奇函数，故f’(0)=0，从而(D)成立．其他三个命题都不正确．
(A)不正确，条件中缺少f(x)在点x=x0处连续，例如
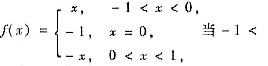x＜0时，f’(x)＞0；当0
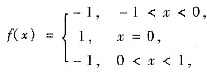显然不满足(B)的结论．
(C)不正确，例如f(x)=1，-1＜x＜1，显然不满足(C)的结论．