问题
问答题
证明:
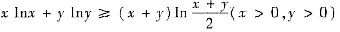 .
.
答案
参考答案:[证] 对任意的x>0,y>0,将f(x)=tlnt在
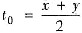 处展开为一阶泰勒公式
处展开为一阶泰勒公式
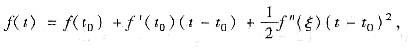
由于当t>0时
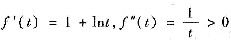 ,所以当t>0时,
,所以当t>0时,
f(t)>f(t0)+f’(t0])(t-t0).
上式中令t分别取x,y得
f(x)>f(t0)+f’(t0)(x-t0), ①
f(y)>f(t0)+f’(t0)(y-t0). ②
①+②得
f(x)+f(y)>2f(t0)+f’(t0)(x+y-2t0),
即
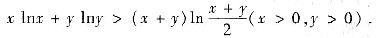
解析: 对于凹凸弧有以下结论:若f(x)在(a,b)内二阶可导,且f"(x)>0(或<0),则
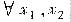 ∈(a,b)且x1≠x2有
∈(a,b)且x1≠x2有
f(x1)>(或<)f(x2)+f’(x2)(x1-x2); (*)
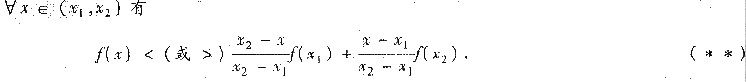
其中(*)表明当曲线为凹弧(或凸弧)时除切点外曲线总在曲线上任一点处的切线之上(或之下);(**)表明当曲线为凹弧(或凸弧)时联结曲线上任二点间的割线总在该段曲线之上(或之下).这就是凹凸弧的几何特征.
