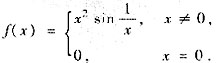问题
单项选择题
设ab＜0，且f(x)在[a，b]上连续，在(a，b)内除x=0外f’(x)存在，又
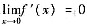，则
(A) x=0是f(x)的极值点．
(B) x=0是f(x)的驻点但非极值点．
(C) (0，f(0))是曲线y=f(x)的拐点．
(D) x=0既非f(x)的驻点或极值点，(0，f(0))也不是曲线y=f(x)的拐点．
答案
参考答案：B
解析： 任意x∈(a，b)，x≠0，则f(t)在以t=0，t=x为端点的闭区间上满足拉格朗日中值定理的条件，所以有
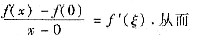
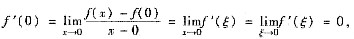
由此可知x=0是f(x)的驻点．
令f(x)=1，则可说明(A)，(C)都不对．故应选(B)．
[评注] 解答此题时我们用拉格朗日中值定理推出了以下结论：
设f(x)在[a，b]上连续，x0∈(a，b)，若f(x)在(a，b)内除x0外都可导，且
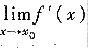存在则f(x)在x0点可导，且
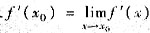；若
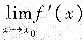不存在，则f(x)在x0点处不一定可导例如．
