参考答案：[证] 由于

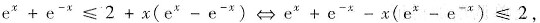
令f(x)=e^x+e^-x-x(e^x-e^-x)，则f(x)=-x(e^x+e^-x)

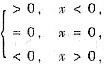所以f(0)是函数f(x)在其定义域内的最大值，且f(0)=2．
从而当x∈(-∞，+∞)时，f(x)≤2，即e^x+e^-x-x(e^x-e^-x)≤2，因此
e^x+e^-x≤2+x(e^x-e^-x)．

解析： 证明函数与数值之间的不等式(f(x)≤m，x∈I)，一般利用最大、最小值来完成，即求f(x)在区间，上的最大或最小值，即可得到所证明的不等式．