如图甲所示,MNCD为一足够长的光滑绝缘斜面,EFGH范围内存在方向垂直斜面的匀强磁场,磁场边界EF、HG与斜面底边MN(在水平面内)平行.一正方形金属框abcd放在斜面上,ab边平行于磁场边界.现使金属框从斜面上某处由静止释放,金属框从开始运动到cd边离开磁场的过程中,其运动的v-t图象如图乙所示.已知金属框电阻为R,质量为m,重力加速度为g,图乙中金属框运动的各个时刻及对应的速度均为已知量,求:
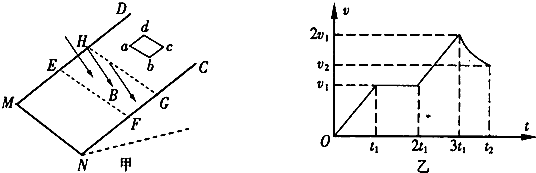
(1)斜面倾角的正弦值和磁场区域的宽度;
(2)金属框cd边到达磁场边界EF前瞬间的加速度;
(3)金属框穿过磁场过程中产生的焦耳热.
(1)由图乙可知,在0~t1时间内金属框运动的加速度
a1=v1 t1
设斜面的倾角θ,由牛顿第二定律有 a1=gsinθ
解得 sinθ=v1 gt1
在t1~2t1时间内金属框匀速进入磁场,则 l0=v1t1
在2t1~3t1时间内,金属框运动位移 s=3v1t1 2
则磁场的宽度 d=l0+s=5v1t1 2
(2)在t2时刻金属框cd边到达EF边界时的速度为v2,设此时加速度大小为a2,
cd边切割磁场产生的电动势 E=Bl0v2
受到的安培力 F=BEl0 R
由牛顿第二定律 F-mgsinθ=ma2
金属框进入磁场时 mgsinθ=B2v12l0 R
解得 a2=v2-v1 t1
加速度方向沿斜面向上.
(3)金属框从t1时刻进入磁场到t2时刻离开磁场的过程中,由功能关系得mg(d+l0)•sinθ=
m1 2
-v 22
m1 2
+Qv 21
解得 Q=4m
-v 21
m1 2
地v 22
答:(1)斜面倾角的正弦值等于
,磁场区域的宽度s=v1 gt1
;5v1t1 2
(2)金属框cd边到达磁场边界EF前瞬间的加速度大小为
,方向沿斜面向上.v2-v1 t1
(3)金属框穿过磁场过程中产生的焦耳热 Q=4m
-v 21
m1 2
.v 22
