若f(x)二阶可导,且
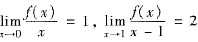 ,试证:
,试证:
(Ⅰ) 存在ξ∈(0,1),使得f(ξ)=0;
(Ⅱ) 存在η∈(0,1),使得f"(η)-f(η)=0.
参考答案:由于
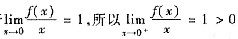 ,根据极限的保号性定理,存在δ>0,当x∈(0,δ)时,恒有
,根据极限的保号性定理,存在δ>0,当x∈(0,δ)时,恒有
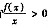 ,从而存在c∈(0,δ),使得f(C)>0.
,从而存在c∈(0,δ),使得f(C)>0.
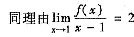 可得:存在1>d>c,使得f(d)<0.
可得:存在1>d>c,使得f(d)<0.
对f(x)在[c,d]上使用零点定理可得:存在
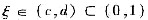 ,使得f(ξ)=0.
,使得f(ξ)=0.
(Ⅱ) 欲证结论
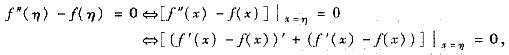
因此可构造辅助函数F(x)=ex[f’(x)-f(x)],这样只需找到ξ1。ξ2∈(0,1),使得
f’(ξi)=f(ξi)(i=1,2).
由于
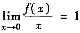 ,所以f(0)=0;又由
,所以f(0)=0;又由
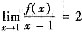 可得f(1)=0.
可得f(1)=0.
令g(x)=e-xf(x),对g(x)分别在区间[0,ξ],[ξ,1]上使用罗尔中值定理可得:存在ξ1∈(0,ξ),ξ2∈(ξ,1),使得g’(ξ1)=0,g’(ξ2)=0,从而f’(ξi)=f(ξi)(i=1,2).
对F(x)=ex[f’(x)-f(x)]在区间[ξ1,ξ2]上使用罗尔定理可得:存在
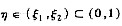 ,使得F’(η)=0,即f"(η)-f(η)=0.
,使得F’(η)=0,即f"(η)-f(η)=0.