问题
问答题
证明：当x＞0时，(x2-1)lnx≥2(x-1)2．
答案
参考答案：[证法一] 令f(x)=(x2-1)lnx-2(x-1)2，则有f(1)=0，且
由此可知：f"(x)在x=1达到最小值，从而有f"(x)＞f"(1)=0(x＞0，x≠1)
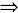f’(x)在(0，+∞)上单调增加，且
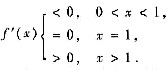这又推出f(x)在x=1达到最小值．从而f(x)＞f(1)=0(x＞0，x≠1)，所以当x＞0时，(x2-1)lnx≥2(x-1)2．
[证法二] 因
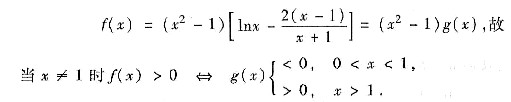
又因g(1)=0，可见只需证g(x)当x＞0时单调增加．计算可得
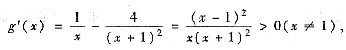
即g(x)在(0，+∞)上单调增加得证．