问题
问答题
若函数f(x)在[0，+∞)上连续，在(0，+∞)内可导，且
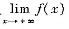存在且为A，又f(0)=A，求证：存在ξ∈(0，+∞)，使f’(ξ)=0．
答案
参考答案：[证] 若f(x)在[0，+∞)恒为常数A，则f’(x)=0，结论成立．故可设f(x)≠A，若存在c∈(0，+∞)，f(C)≠A，不妨设f(C)＞A．
因为
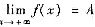，故必存在a＞c，使
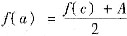．(否则，由介值定理，x＞c时，f(x)＞
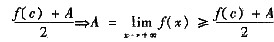，与f(C)＞A的似设相矛盾．)
又函数f(x)在[0，c]上连续，
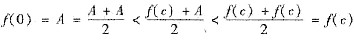，故由介值定理可知，存在b∈(0，c)，使
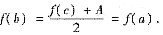
由于f(x)在区间[a，b]上满足罗尔定理的条件，故存在
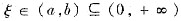，使f’(ξ)=0．
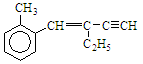下列结论正确的是