问题
填空题
函数
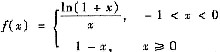 的单减区间是______.
的单减区间是______.
答案
参考答案:(-1,+∞)
解析: 由f(x)的分段表示知:f(x)分别在(-1,0)和[0,+∞)上连续,又所以f(x)在(-1,+∞)上连续.又
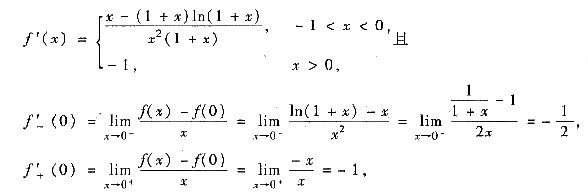
所以f’(0)不存在.
从而定义域内导数为零和导数不存在的点只有x=0(因为若设g(x)=x-(1+x)ln(1+x),则g(0)=0,g’(x)=-ln(1+x),当-1<x<0时,g’(x)>0,所以当-1<x<0时,g(x)<0,故没有导数为零的点).
由于当-1<x<0时,f’(x)<0,因此函数在区间(-1,0]上单调递减;当x>0时,f’(x)<0,所以函数在区间[0,+∞)内单调递减.故函数单渊减少区间为(-1,+∞).
