问题
单项选择题
设f(x)在x=0的某邻域内有二阶连续导数,且f’(0)=0,
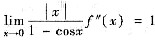 ,则
,则
(A) f(0)是f(x)的极大值.
(B) f(0)是f(x)的极小值.
(C) (0,f(0))是曲线y=f(x)的拐点.
(D) x=0不是f(x)的极值点,(0,f(0))也不是曲线y=f(x)的拐点.
答案
参考答案:B
解析: 由于
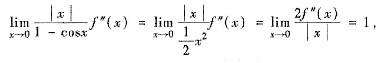
由极限的保号性可知在x=0的某邻域内必有f"(x)>0,即知f’(x)在该邻域内为单调增加,又因f’(0)=0,于是f’(x)在x=0两侧变号,即f(x)在x=0两侧改变增减性,且当x<0时,f’(x)>0,f(x)单捌减少;当x>x0时,f’(x)>0,f(x)单调增加.故点x=0为f(x)的极小值点.应选(B).
