问题
问答题
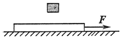
如图所示,质量M=10kg,上表面光滑的足够长的木板在水平拉力F=20N的作用下,以υ0=5m/s的初速度沿水平地面向右匀速运动,现有足够多的小铁块,它们质量均为m=1kg,将一铁块无初速地放在木板最右端,当木板运动了L=1m时,又无初速地在木板最右端放上第二个铁块,以后只要木板运动了L就在木板最右端无初速放一铁块(g=10m/s2).求:
(1)第一个铁块放上后,木板运动1m时,木板的速度多大?
(2)最终有几个铁块能留在木板上?
(3)最后一个铁块与木板右端距离多大?
答案
(1)由F=μMg 得μ=0.5①
第一个铁块放上后,木板做匀减速运动,由动能定理得:
μmgL=
Mv02-1 2
Mv12②1 2
代入数据得v1=2
m/s6
(2)对木板有F合=f-F=nμmg③
第一个铁块放上后μmgL=
Mv02-1 2
Mv12④1 2
第二个铁块放上后2μmgL=
Mv12-1 2
Mv22⑤1 2
…
第n个铁块放上后nμmgL=
Mvn-12-1 2
Mvn2⑥1 2
由④⑤⑥式得(1+2+3+…+n)μmgL=
Mv02-1 2
Mvn2⑦1 2
木板停下时vn=0,得n=6.6,
所以最终有7个铁块能留在木板上
(3)设当第7块铁块放上后,最后静止的位置距木板右端的距离为d由第(2)问得:
μmgL+7μmgd=6×(6+1) 2
Mv021 2
解得d=
m4 7
答:(1)第一个铁块放上后,木板运动1m时,木板的速度为2
m/s.6
(2)最终有7个铁块能留在木板上
(3)最后一个铁块与木板右端距离为
m.4 7