问题
问答题
设函数f(x)在闭区间[0，1]上连续，在开区间(0，1)内可导，且
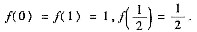
证明：对任何满足0＜k＜1的常数k，存在ξ∈(0，1)，使．f’(ξ)=-k．
答案
参考答案：[证] 令F(x)=f(x)+kx，则F(x)在[0，1]上连续，在(0，1)内可导，且
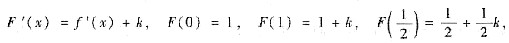
从而
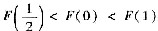，根据闭区间上连续函数的性质得：存在
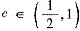，使得F(C)=F(0)，从而F(x)在闭区间[0，c]上满足罗尔定理的条件，于是存在
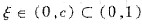，使F’(ξ)=f’(ξ)+k=0，即f"(ξ)=-k．
解析： 设函数f(x)满足某些条件，证11月(a，b)内至少存在一点ξ，使得f’(ξ)=h(ξ)．这类命题解题的一般思路为：先构造辅助函数F(x)，然后找[a，b]的一个子区间[x1，x2]，使得F(x1)=F(x2)，最后对F(x)在[x1，x2]上使用罗尔中值定理即可．