问题
填空题
设函数f(x)有反函数g(x)，且f(a)=3，f’(a)=1，f"(a)=2，则g"(3)=______．
答案
参考答案：-2
解析： 记y=f(x)，应注意到，g(x)为f(x)的反函数，已经改变了变量记号，为了利用反函数导数公式，必须将g(x)改写为g(y)．
将等式f’(x)g’(y)=1两边关于x求导得
f"(x)g’(y)+f’(x)"(y)y’x=0，
或f"(x)g’(y)+[f’(x)]2g"(y)=0．
注意到
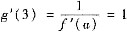，在上式中令x=a，应有y=3，因此得到
g"(3)=-f"(a)g’(3)=-2．