问题
单项选择题
设f(x)在x0可导且f’(x0)＞0，则存在δ＞0，使得
(A) f(x)在(x0-δ，x0+δ)内单调上升．
(B) f(x)＞f(x0)，x∈(x0-δ，x0+δ)，x≠x0．
(C) d(x)＞f(x0)，x∈(x0，x0+δ)．
(D) f(x)＜f(x0)，x∈(x0，x0+δ)．
答案
参考答案：C
解析： 根据导数的定义
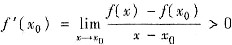，由极限的保号性定理可得：存在δ＞0，当0＜|x-x0|＜δ时，
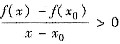．特别，当0＜x-x0＜δ即x0＜x＜x0+δ时，f(x)-f(x0)＞0，所以(C)正确，(B)、(D)不正确．
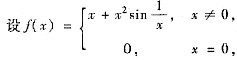用定义可求得：f’(0)=1＞0，但f(x)在含x=0的任意小区间(-δ，δ)内不是单调上升的，故(A)不正确．因此应选(C)．