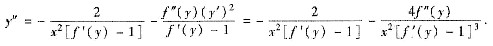问题
问答题
设函数f(x)具有二阶导数，且f’≠0，求由方程x2ey=ef(y)确定的隐函数y=y(x)的一阶、二阶导数．
答案
参考答案：原方程两端取对数得：2In|x|+y=f(y)，将此方程两端对x求导得
(*)
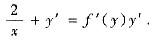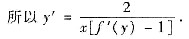
将(*)式两端再对x求导即得
搜题请搜索小程序“爱下问搜题”
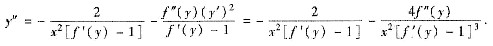
设函数f(x)具有二阶导数，且f’≠0，求由方程x2ey=ef(y)确定的隐函数y=y(x)的一阶、二阶导数．
参考答案：原方程两端取对数得：2In|x|+y=f(y)，将此方程两端对x求导得
(*)
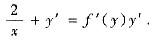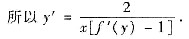
将(*)式两端再对x求导即得