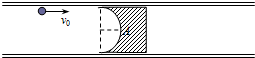
如图,是固定在水平面上的横截面为“

”形的光滑长直导轨槽,槽口向上,槽内放置一金属滑块,滑块上有半径为R的半圆柱形光滑凹槽,金属滑块的宽度为2R,比“

”形槽的宽度略小.现有半径为r(r<<R)的金属小球以水平初速度v0冲向滑块,从滑块上的半圆形槽口边缘进入.已知金属小球的质量为m,金属滑块的质量为3m,全过程中无机械能损失.求:
(1)当金属小球滑离金属滑块时,金属小球和金属滑块的速度各是多大;
(2)当金属小球经过金属滑块上的半圆柱形槽的底部A点时,对金属滑块的作用力是多大.
(1)小球与滑块相互作用过程中,沿水平方向动量守恒,则有:mv0=mv1+3mv2
又因为系统机械能守恒:
m1 2
=v 20
m1 2
+v 21
3m1 2 v 22
得 v1=-
v0,方向向左.v2=1 2
v0,方向向右.1 2
(2)当金属小球通过A点时,沿导轨方向金属小球与金属滑块具有共同速度v,沿A点切线方向的速度为v′,由动量守恒和机械能守恒得
mv0=(m+3m)v
m1 2
=v 20
(m+3m)v2+1 2
mv′21 2
解得 v′=
v03 2
由牛顿第二定律得N=
=mv′2 R 3m v 20 4R
即为对金属块的作用力大小为3m v 20 4R
答:
(1)当金属小球滑离金属滑块时,金属小球的速度大小是
v0,方向向左,金属滑块的速度大小为1 2
v0,方向向右.1 2
(2)当金属小球经过金属滑块上的半圆柱形槽的底部A点时,对金属滑块的作用力是
.3m v 20 4R
