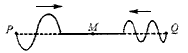问题
填空题
试说明下列事实的几何意义：
(1) 看函数f(x)，g(x)在x0可导且f(x0)=g(x0)，f’(x0)=g’(x0)，则其几何意义是______；
(2) 若函数f(x)在x0存在f’+(x0)，f’-(x0)，但f’+(x0)≠f’-(x0)，则其几何意义是______；
(3) 若函数f(x)在x=x0连续，又
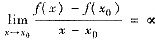，则其几何意义是______．
答案
参考答案：(1) 曲线y=f(x)与y=g(x)在M0点处相切
(2) 曲线y=f(x)在M0处的左、有切线有一个夹角
(3) 割线趋于垂直方向，曲线y=f(x)在点M0有垂直于x轴的切线x=x0
解析： (1) f(x0)=g(x0)表示曲线y=f(x)与y=g(x)有交点M0(x0，f(x0))，即(x0，g(x0))，又f’(x0)=g’(x0)，表示曲线在交点处切线的斜率相同．因此曲线y=f(x)与y=g(x)在M0点处相切．
(2) 函数y=f(x)在x=x0存在极限
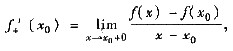
表示点M(x，f(x))在M0(x0，(x0))右方沿曲线y=f(x)趋于M0时割线
的斜率的极限为f’+(x0)，它是曲线y=f(x)在点M0处的有切线的斜率．同理，f’-(x0)是曲线)y=f(x)在点M0处左切线的斜率．f’+(x0)≠f’-(x0)即曲线y=f(x)在M0处的左、有切线有一个夹角．见图2-5．
(3) y=f(x)在x=x0连续表示x→x0时，点M(x，f(x))沿曲线y=f(x)趋于点M0(x0，f(x0))．而
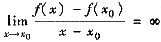表示点M沿曲线趋于M0时割线
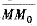的斜率趋于∞，即割线趋于垂直方向，曲线y=f(x)在点M0有垂直于x轴的切线x=x0．见图2-6．
