问题
单项选择题
设k为常数，函数y=f(x)在点x=x0处的增量满足
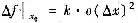，其中△x是自变量x的增量，则函数y=f(x)在x0处
(A) 连续，不一定可微． (B) 可微，且f(x0)=k．
(C) 可微，且f’(x0)=0． (D) 可微，且f’(x0)=1．
答案
参考答案：C
解析： 由于函数改变量的线性主部为零，而k·o(△x)是△x的高阶无穷小量，按可微的定义知f(x)在点x=x0处可微，因而可导，且导数值f’(x0)=0，因此选(C)．