问题
单项选择题
设
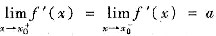，则下列结论正确的是
(A)
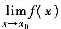未必存在．
(B) f(x)在x=x0处必连续，但未必可导．
(C)
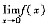存在，但f(x)在x=x0处未必连续．
(D) f(x)在x=x0处必可导且f’(x0)=a．
答案
参考答案：A
解析： 首先将f(x)在x=x0处的左、有导数
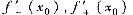与f’(x)在x=x0处的左、右极
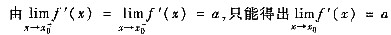，但不能保证f(x)在x=x0处可导，以及f(x)在x=x0处连续和极限存在．
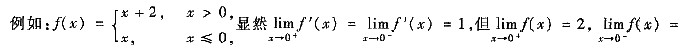0，因此极限
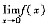不存在．因此选(A)．
[评注] 如果f(x)在(a，b)内连续，x0∈(a，b)，且设
则f(x)在x=x0处必可导且f’(x0)=m(此结论可用左、右导数的定义并结合拉格朗日中值定理推出)．