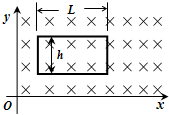
如图所示，在粗糙绝缘的水平面内，存在一竖直向下的磁场区域，磁

问题问答题

如图所示，在粗糙绝缘的水平面内，存在一竖直向下的磁场区域，磁感强度B沿水平向右的方向均匀增加．若在该磁场区域内建立直角坐标系xoy，则磁感强度B的分布规律可表示为B=kx（x的单位为m，B的单位为T）．有一个长为L、宽为h、质量为m、电阻为R的不变形的矩形金属线圈，在运动过程中始终位于磁场区域内．当它在该平面内运动时，将受到大小恒为 f 的阻力作用．

（1）要让线圈在水平外力F的作用下，从静止开始向右做加速度为a的匀加速直线运动，求F随时间t的变化规律．

（2）若磁场区域以速度v₁水平向左匀速运动，线圈从静止开始释放，求此后线圈运动的最大速度．

（3）若零时刻磁场区域由静止开始水平向左做匀加速直线运动，同时线圈从静止开始释放，已知在经一段足够长的时间后，t时刻磁场区域的速度为v_t，求t时刻线圈的速度．

答案

（1）设线圈的右边导线所在位置的磁感应强度为B₁、左边导线所在位置的磁感应强度为B₂，则E=B₁hv-B₂hv=kLhv

线圈所受的安培力 F_A=（B₁-B₂）

由牛顿第二定律可得：F-F_A-f=ma

即得 F-(B1-B2)

h-f=ma

又 v=at

得，F随时间t的变化规律为 F=ma+f+

(kLh)2

（2）若FA=

(kLh)2v

≤f时，线圈将始终静止不动．

若FA=

(kLh)2v

＞f时，线圈将加速度向左动，最终匀速．

设线圈匀速时的速度为v′，则有

(kLh)2(v-v′)

解得 v′=v-

(kLh)2

（3）线圈的加速度最终与磁场的加速度相同，即 a=

．

设t时刻线圈的速度为v″，则

(kLh)2(vt-v″)

-f=ma

解得

v″=v_t-

(f+m

(kLh)2

答：

（1）要让线圈在水平外力F的作用下，从静止开始向右做加速度为a的匀加速直线运动，F随时间t的变化规律为 F=ma+f+

(kLh)2

at．

（2）若磁场区域以速度v₁水平向左匀速运动，线圈从静止开始释放，此后线圈运动的最大速度v-

(kLh)2

．

（3）t时刻线圈的速度为v_t-

(f+m

(kLh)2

．