如图所示,空间存在磁感应强度为B,方向竖直向下的匀强磁场,MN、PQ是相互平行的粗糙的长直金属导轨,处于同一水平面内,间距为L,电阻不计,在导轨左端连有电阻、电源和单刀双掷开关,电阻阻值为R,电源电动势为E,内阻为r;ab是垂直跨接在导轨上质量为m、电阻也为R的导体棒,它与导轨间的动摩擦因数μ.单刀双掷开关扳到1时,导体棒由静止开始向右加速运动,求:
(1)导体棒的最大加速度和最大速度各是多少?
(2)导体棒达到最大加速度时,导体棒消耗的电功率P是多少?
(3)导体棒达到最大速度后,把单刀双掷开关掷向2,导体棒再运动时间t后静止,则导体棒减速运动的位移是多少?
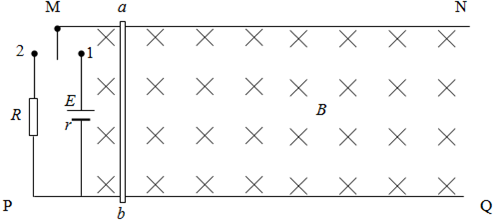
(1)在刚闭合电键时加速度最大
根据牛顿第二定律有:mam=F-f
F=B
L,E R+r
联立解得 am=
-μgBEL m(R+r)
当安培力与摩擦力相等时速度最大有:
F′=f BIminL=μmg B
L=μmgE-BLvm R+r
解得 vm= BLE-μmg(R+r) B2L2
(2)刚闭合电键时加速度最大,此时电路中的电流I=E R+r
则导体棒上消耗的功率P=I2R=E2R (R+r)2
(3)导体棒在减速运动的过程中安培力的冲量
I=
BI1L△t1+BI2L△t2…= 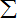
B 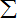
L△t1+BBLv1 2R
L△t2••=BLv2 2R B2L2s 2R
根据动量定理有:
+μmgt=mvmB2L2s 2R
+μmgt=mB2L2s 2R BLE-μmg(R+r) B2L2 s=2mR BLE-μmg(R+r)-μgtB2L2 B4L4
答:(1)导体棒的最大加速度和最大速度各是
、
-μgBEL m(R+r)
. BLE-μmg(R+r) B2L2
(2)导体棒达到最大加速度时,导体棒消耗的电功率P是
.E2R (R+r)2
(3)导体棒减速运动的位移是
. s=2mR BLE-μmg(R+r)-μgtB2L2 B4L4
