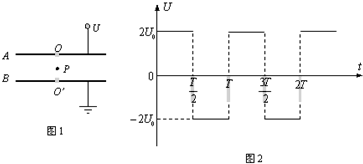
如图1所示,A、B为水平放置的平行金属板,板间距离为d(d远小于板的长和宽).在两板的中心各有小孔O和O’,O和O’处在同一竖直线上.在两板之间有一带负电的质点P.已知A、B间所加电压为U0时,质点P所受的电场力恰好与重力平衡.现在A、B 间加上如图2所示随时间t作周期性变化的电压U,已知周期T=
(g为重力加速度).在第一个周期内的某一时刻t0,在A、B 间的中点处由静止释放质点P,一段时间后质点P从金属板的小孔飞出.12d g
(1)t0在什么范围内,可使质点在飞出小孔之前运动的时间达到最短?
(2)t0在哪一时刻,可使质点P从小孔飞出时的速度达到最大?
设质点P的质量为m,电量大小为q,根据题意,当A、B间的电压为U0时,有
q
=mg U0 d
当两板间的电压为2U0时,P的加速度向上,其大小为a1,则
q
-mg=ma1 解得 a1=g U0 d
当两板间的电压为-2U0时,P的加速度向下,其大小为a2,则
q
+mg=ma2 解得 a2=3g U0 d
(1)要使质点在飞出小孔之前运动的时间达到最短,须使质点释放后一直向下加速运动.设质点释放后经过时间t到达小孔O′,则
d=1 2
a2t2 解得 t=1 2 d 3g
因为周期T=
,所以t<12d g T 2
质点到达小孔之前能一直加速.因此要使质点在飞出小孔之前运动的时间达到最短,质点释放的时刻t0应
满足
≤t0≤T-t,即T 2
≤t0≤53d g d 3g
(2)要使质点P从小孔飞出时的速度达到最大,须使质点释放后先向上加速、再向上减速运动,在到达小孔O时速度减为0,然后向下加速运动直到小孔O’.
设质点释放后向上加速时间为t1、向上减速时间为t2,则
v1=gt1 0=v1-3gt2
d=1 2
g1 2
+(v1t2-t 21
3g1 2
) t 22
由以上各式解得
t1=
t2=3d 4g d 12g
因为t1<
,t2<T 2 T 2
因此质点P能向上先加速后减速恰好到达小孔O.设质点从小孔O向下加速运动到小孔O’经过的时间为t3,则
d=
3g1 2 t 23
解得t3=2d 3g
因为t2+t3=(1+2
)2 2 3
<d g
,因此质点P能从小孔O向下一直加速运动到小孔O’,T 2
此时质点P从小孔O’飞出时的速度达到最大.因此,要使质点P从小孔飞出时的速度达到最大,质点P释放的时刻应为
t0=
-t1=T 2 3d 4g
故答案为:(1)
≤t0≤53d g
(2)d 3g 3d 4g
