如图甲所示,两根足够长的光滑平行金属导轨相距为L=0.40m,导轨平面与水平面成θ=30?角,上端和下端通过导线分别连接阻值R1=R2=1.2Ω的电阻,质量为m=0.20kg、阻值为r=0.20Ω的金属棒ab放在两导轨上,棒与导轨垂直且保持良好接触,整个装置处在垂直导轨平面向上的磁场中,取重力加速度g=10m/s2.若所加磁场的磁感应强度大小恒为B,通过小电动机对金属棒施加力,使金属棒沿导轨向上做匀加速直线运动,经过0.5s电动机的输出功率达到10W,此后保持电动机的输出功率不变,金属棒运动的v-t图如图乙所示,试求:
(1)磁感应强度B的大小;
(2)在0-0.5s时间内金属棒的加速度a的大小;
(3)在0-0.5s时间内电动机牵引力F与时间t的关系;
(4)如果在0-0.5s时间内电阻R1产生的热量为0.135J,则这段时间内电动机做的功.
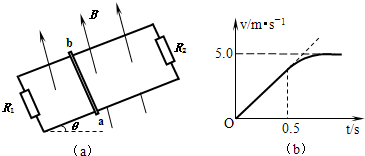
(1)由图象可知,当金属棒的最大速度为vm=5m/s,因为此时电动机的功率恒为P=10W,根据P=Fv可得此时电动机对金属棒的拉力F=
①P vm
对金属棒进行受力分析可得:
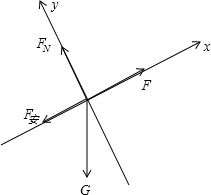
由图可知:F合x=F-F安-mgsin30°=0
故此时F安=F-mgsinθ ②
又因为回路中产生的感应电动势E=BLvm ③
根据欧姆定律可得,此时回路中电流I=
④BLvm r+ R 2
由①②③④可解得B=1T
(2)由题意可知,当t=0.5s时,金属棒获得的速度v=at
此时电路中产生的感应电流I=
,金属棒受到的安培力=F安=BLv r+
R1 2 B2L2v r+
R1 2
此时电动机的拉力F=P v
则对金属棒进行受力分析有:F-F安-mgsinθ=ma
代入有关数据有:
-P at
-mgsinθ=maB2L2at r+
R1 2
又因为t=0.5s,m=0.2kg,R=1.2Ω,r=0.20Ω,θ=30°
所以可计算得a=
m/s220 3
(3)在0-0.5s时间里对金属棒进行受力分析有:
F-F安-mgsinθ=ma得
F=ma+mgsin30°+F安
代入a=
m/s2,F安=20 3
,m=0.2kg,R=1.2Ω,r=0.20Ω,θ=30°B2L2v r+
R1 2
可计算得F=
+4t 3
.7 3
(4)令通过导体棒的电流为I,则通过电阻R1和R2的电流分别为
I1 2
电流做功Q=I2Rt得:
对于R1产生的热量:Q1=(
)2RtI 2
对于R2产生的热量:Q2=(
)2RtI 2
对于导体棒r产生的热量:Q3=I2rt
因为I和t相等,R=1.2Ω,r=0.2Ω,Q1=0.135J
所以可以计算出:Q2=Q1=0.135J,Q3=0.09J
即整个电路产生的热量Q=Q1+Q2+Q3=0.36J
对整个0.5s过程中由于导体棒的加速度为
m/s2在0.5s的时间里,导体棒沿轨道上升的距离20 3
x=
at2=1 2
×1 2
×(20 3
)2m=1 2
m5 6
0.5s末导体棒的速度v=at=
×20 3
m/s=1 2
m/s10 3
在这0.5s的时间里,满足能量守恒,故有:
WF-Q-mgxsinθ=
mv21 2
∴力F做功为:WF=Q+mgxsinθ+
mv21 2
代入Q=0.36J,m=0.2kg,x=
m,v=5 6
m/s可得:10 3
WF=2.34J
答:(1)磁感应强度B=1T;
(2)在0-0.5s时间内金属棒的加速度a=
m/s2;20 3
(3)在0-0.5s时间内电动机牵引力F与时间t的关系:F=
+4t 3
;7 3
(4)如果在0-0.5s时间内电阻R1产生的热量为0.135J,则这段时间内电动机做的功WF=2.34J.
