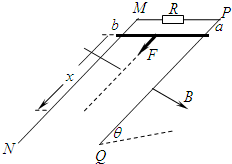
如图所示,两根足够长的光滑直金属导轨MN、PQ平行固定在倾角θ=37°的绝缘斜面上,两导轨间距L=1m,导轨的电阻可忽略.M、P两点间接有阻值为R 的电阻.一根质量m=1kg、电阻r=0.2Ω的均匀直金属杆ab放在两导轨上,与导轨垂直且接触良好.整套装置处于磁感应强度B=0.5T的匀强磁场中,磁场方向垂直斜面向下.自图示位置起,杆ab受到大小为F=0.5v+2(式中v为杆ab运动的速度,力F的单位为N)、方向平行导轨沿斜面向下的拉力作用,由静止开始运动,测得通过电阻R的电流随时间均匀增大.g取10m/s2,sin37°=0.6.
(1)试判断金属杆ab在匀强磁场中做何种运动,并请写出推理过程;
(2)求电阻的阻值R;
(3)求金属杆ab自静止开始下滑通过位移x=1m所需的时间t和该过程中整个回路产生的焦耳热Q.
(1)金属杆做匀加速运动(或金属杆做初速为零的匀加速运动).
通过R的电流I=
=E R+r
,因通过R的电流I随时间均匀增大,即杆的速度v随时间均匀增大,杆的加速度为恒量,故金属杆做匀加速运动.BLv R+r
(2)对杆,根据牛顿第二定律有:F+mgsinθ-BIL=ma
将F=0.5v+2代入得:
2+mgsinθ+(0.5-
)v=ma,B2L2 R+r
因a与v无关,所以
a=
=8m/s22+mgsinθ m
代入得0.5-
=0 得B2L2 R+r
R=0.3Ω
(3)由x=
at2得,所需时间t=1 2
=0.5s2x a
在极短时间△t内,回路产生的焦耳热为
△Q=
△t=(BLv)2 R+r
△t=32t2△t(BLat)2 R+r
在t=0.5s内产生的焦耳热Q=
32t2△t= 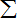
×(0.5)3J=32 3
J4 3
答:
(1)金属杆ab金属杆做匀加速运动.
(2)电阻的阻值R=0.3Ω;
(3)金属杆ab自静止开始下滑通过位移x=1m所需的时间t=0.5s,该过程中整个回路产生的焦耳热Q=
J.4 3
