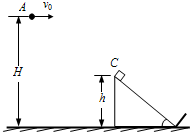
如图所示,一弹丸从离地高度H=1.95m的A点以v0=8.0m/s的初速度水平射出,恰以平行于斜面的速度射入静止在固定斜面顶端C处的一木块中,并立即与木块具有相同的速度(此速度大小为弹丸进入木块前一瞬间速度的
)共同运动,在斜面下端有一垂直于斜面的挡板,木块与它相碰没有机械能损失,碰后恰能返回C点.已知斜面顶端C处离地高h=0.15m,求:1 10
(1)A点和C点间的水平距离;
(2)木块与斜面间的动摩擦因数μ;
(3)木块从被弹丸击中到再次回到C点的时间t.
(1)弹丸从A到C做平抛运动,则有:
t=
=0.6s2(H-h) g
A点到C点的水平距离s=v0t=8.0×0.6m=4.8m
(2)设弹丸到C的速度方向与水平方向的夹角为θ,则
tgθ=
=vy v0
=10×0.6 8 3 4
vC=
=v02+vy2
m/s=10m/s82+62
弹丸与塑料块在C点具有的相同速度vC′=
vC=1m/s 1 10
分析弹丸与塑料块从C点返回到C点的整个过程,根据动能定理有:
-μmgcosθ×2×
=0-h sinθ
mvC′21 2
可得动摩擦因数μ=
=0.1251 8
(3)根据牛顿第二定律,
下滑时由 a1=gsinθ-μgcosθ
可得a1=5 m/s2
由
=vC′t1+h sinθ
a1 t121 2
可解得t1=0.17s
上滑时由 a1=gsinθ+μgcosθ
可得a2=7 m/s2
由
=h sinθ
a2t221 2
可解得t2=0.27s
所以塑料块从被弹丸击中到再次回到C点的时间t=t1+t2=0.44s
答:(1)A点和C点间的水平距离为4.8m;
(2)木块与斜面间的动摩擦因数μ为0.125;
(3)木块从被弹丸击中到再次回到C点的时间t为0.44s.

