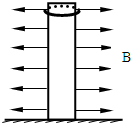
如图所示,很长的光滑磁棒竖直固定在水平面上,在它的侧面有均匀向外的辐射状的磁场.磁棒外套有一个质量均匀的圆形线圈,质量为m,半径为R,电阻为r,线圈所在磁场处的磁感应强度为B.让线圈从磁棒上端由静止释放沿磁棒下落,经一段时间与水平面相碰并反弹,线圈反弹速度减小到零后又沿磁棒下落,这样线圈会不断地与水平面相碰下去,直到停留在水平面上.已知第一次碰后反弹上升的时间为t1,下落的时间为t2,重力加速度为g,不计碰撞过程中能量损失和线圈中电流磁场的影响.求:
(1)线圈第一次下落过程中的最大速度υm
(2)第一次与水平面碰后上升到最高点的过程中通过线圈某一截面的电量q
(3)线圈从第一次到第二次与水平面相碰的过程中产生的焦耳热Q.
(1)线圈第一次下落过程中有E=B•2πRv、I=、FA=BIL=BI•2πR,得安培力大小为 FA=
根据牛顿第二定律得 mg-FA=ma
可知线圈做加速度减小的加速运动,当a=0时,速度最大,代入求得最大速度为:υm=
(2)反弹后上升的过程中某一时刻,由牛顿运动定律得:mg+BI•2πR=ma
则得:mg△t+BI•2πR•△t=ma△t
在一段微小时间△t内,速度增量为△υ=a△t,通过线圈截面电量为:△q=I△t
则:△q=
得到:∑△q=,又ma△t=m△v=mvm=,mg△t=mgt1,
故:q=-
(3)反弹后上升的过程中某一时刻,由牛顿运动定律得:mg+B×2πR=ma
在一段微小时间△t内,速度增量为:△υ=a△t,线圈上升高度为:△h=υ△t
则线圈可上升的最大高度h为:h=∑△h=r=-
线圈到达最高点后,下落过程中的某一时刻,由牛顿运动定律得:mg-B×2πR=ma
在一段微小时间△t内,速度增量为:△υ=a△t,线圈下降高度为:△h=υ△t
则线圈第二次下降到水平面时的速度为:υ=∑△υ=∑(mg-)△t=g(t1+t2)-
本过程中线圈中产生的热量为线圈动能的损失:Q=mυm2-mυ2=m()2-m(g(t1+t2)-)2
化简得:Q=(t1+t2)-mg2(t1+t2)2
答:(1)线圈第一次下落过程中的最大速度υm为.
(2)第一次与水平面碰后上升到最高点的过程中通过线圈某一截面的电量q为-.
(3)线圈从第一次到第二次与水平面相碰的过程中产生的焦耳热Q为(t1+t2)-mg2(t1+t2)2.