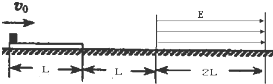
一块质量为m=1Kg,、长为L的木板,静止在光滑的水平面上,一个质量也为m、带正电,且电荷量为q=0.2c的小金属块以水平速度v0=5m/s从木板的左端开始在木板上滑动,此时木板的右端距有界匀强电场的左边距离为L,当木板的右端运动到匀强电场的左边时,金属块与木板恰好相对静止,且位于木板的中间.以后通过匀强电场的过程中金属块与木板仍然相对静止,其中L=1m.重力加速度为g=10m/s2.求:
(1)金属块与木板之间的动摩擦因数为μ=?
(2)匀强电场的强度E的最大不超过多少?
(3)若金属块与木板离开匀强电场后它们的共同速度仍为v0,匀强电场宽为2L.则匀强电场的电场强度E为多少?
(1)设木板进入电场前的共同速度为V,对金属块:
由动能定理:
-μmg
L=3 2
mV2-1 2
mV02 ①1 2
对板:μmgL=
mV2 ②1 2
由上两式得:μ=
=V 20 5gL
=0.5 ③52 5×10×1
(2)木板进入电场后,根据牛顿第二定律得
对金属块:qEm-μmg=ma ④
对木板:μmg=ma ⑤
则最大场强:Em=
=50N/C ⑥2μmg q
(3)将板与金属块为整体,由动能定理得:
qE•2L=
•2mV02-1 2
•2mV2 ⑦1 2
由②⑦式E=37.5N/C⑧
答:(1)金属块与木板之间的动摩擦因数为μ为0.5.
(2)匀强电场的强度E的最大不超过50N/C.
(3)匀强电场的电场强度E为37.5N/C.

