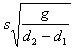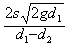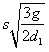问题
选择题
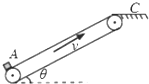
如图所示,工厂利用皮带传输机把货物从地面运送到高出水平地面的C平台上,C平台离地面的高度一定.运输机的皮带以一定的速度v顺时针转动且不打滑.将货物轻轻地放在A处,货物随皮带到达平台.货物在皮带上相对滑动时,会留下一定长度的痕迹.已知所有货物与皮带间的动摩擦因数为μ.若皮带的倾角θ、运行速度v和货物质量m都可以改变,始终满足tanθ<μ.可以认为最大静摩擦力等于滑动摩擦力( )
A.当速度v一定时,角θ越大,运送时间越短
B.当倾角θ一定时,改变速度v,运送时间不变
C.当倾角θ和速度v一定时,货物质量m越大,皮带上留下的痕迹越长
D.当倾角θ和速度v一定时,货物质量m越大,皮带上摩擦产生的热越多
答案
A、物体匀加速运动时,根据牛顿第二定律可得:μmgcosθ-mgsinθ=ma
解得物体的加速度为:a=μgcosθ-gsinθ
角θ越大,加速度越小,皮带x=h sinθ
运送时间可能变短,也有可能变长.
B、当倾角θ一定时,加速度不变,皮带长度不变,速度增大,运送时间越短.故B错误
C、皮带上留下的痕迹△x=vt-
at2 t=1 2 v a
△x=
,当倾角θ和速度v一定时,货物质量m越大,皮带上留下的痕迹不变,故C错误v2 2a
D、皮带上摩擦产生的热Q=f•△x=μmgcosθ•v2 2a
当倾角θ和速度v一定时,加速度不变,货物质量m越大,皮带上摩擦产生的热越多.故D正确
故选D.