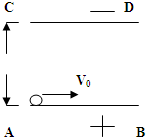
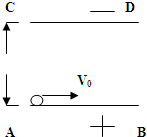
如图所示,带等量异种电荷的两块相互平行的金属板AB、CD长都为L,两板间距为d,其间为匀强电场,当两极板电压U0为时,有一质量为m,带电量为q的质子紧靠AB板上的上表面以初速度V0射入电场中,设质子运动过程中不会和CD相碰,求:
(1)当t=
时,质子在竖直方向的位移是多大?L 2v0
(2)当t=
时,突然改变两金属板的电性,且两板间电压为U1,质子恰能沿B端飞出电场,求:电压U1与U0的比值是多大?L 2v0
(1)质子进入电场的加速度为a=
=F m
=qE m qU0 md
当t=
时,质子在竖直方向的位移:L 2v0
y=
at2=1 2 1 2
(qU0 md
)2=L 2v0 qU0L2 8mdv02
(2)当t=
时,质子在竖直方向的速度:L 2v0
vy=at=qU0 md
=L 2v0 qU02L 2mdv0
改变两极板的极性后,质子在竖直方向上的加速度:
a ′=
=F ′ m
=qE ′ m qU1 md
在竖直方向上,由匀变速直线运动公式,得:
-y=vyt-
a ′t21 2
带入以上各数据,有
-
=qU0L2 8mdv02
(qU02L 2mdv0
)-L 2v0 1 2
(qU1 md
)2L 2v0
解得
=U1 U0 3 1
答:(1)当t=
时,质子在竖直方向的位移为L 2v0
.qU0L2 8mdv02
(2)当t=
时,突然改变两金属板的电性,且两板间电压为U1,质子恰能沿B端飞出电场,则L 2v0
=U1 U0
.3 1
