问题
问答题
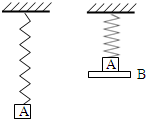
如图所示,轻质弹簧的劲度系数为k,下面悬挂一个质量为m的砝码A,手持木板B托住A缓慢向上压弹簧,至某一位置静止.此时如果撤去B,则A的瞬时加速度为
g.现用手控制B使之以a=8 5
g的加速度向下做匀加速直线运动.求:2 5
(1)砝码A能够做匀加速运动的时间?
(2)砝码A做匀加速运动的过程中,弹簧弹力对它做了多少功?木板B对它的支持力做了多少功?
答案
(1)设初始状态弹簧压缩量为x1
则:kx1+mg=m×
g8 5
解得:x1=3mg 5k
当B以a=
g匀加速向下运动时,由于a<g,所以弹簧在压缩状态时A、B不会分离,设该过程的终止时刻弹簧伸长量为x22 5
则:mg-kx2=m×
g2 5
解得:x2=3mg 5k
A匀加速运动的位移s=x1+x2=6mg 5k
由位移关系式:s=
at21 2
解得:t=6m k
(2)因为x1=x2
这一过程中弹簧对物体A的弹力做功为0
A、B分离时vA=at=
g2 5 6m k
由动能定理得:mgs+WF=
mvA21 2
代入得:WF=-18m2g2 25k
答:
(1)砝码A能够做匀加速运动的时间为6m k
(2)砝码A做匀加速运动的过程中,弹簧弹力对它做为零,木板B对它的支持力做为-18m2g2 25k
