在一水平向右匀速传输的传送带的左端A点,每隔T的时间,轻放上一个相同的工件,已知工件与传送带间动摩擦因素为μ,工件质量均为m,经测量,发现后面那些已经和传送带达到相同速度的工件之间的距离为x,下列判断正确的有( )
A.传送带的速度为x T
B.传送带的速度为22μgx
C.每个工件与传送带间因摩擦而产生的热量为μmgx 2
D.在一段较长的时间t内,传送带因为传送工件而将多消耗的能量为mtx2 T3
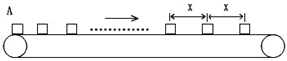
A、工件在传送带上先做匀加速直线运动,然后做匀速直线运动,每个工件滑上传送带后运动的规律相同,可知x=vT,解得传送带的速度v=
.故A正确.x T
B、设每个工件匀加速运动的位移为s,根据牛顿第二定律得,工件的加速度为μg,则传送带的速度v=
=2as
,根据题目条件无法得出s与x的关系.故B错误.2μgs
C、工件与传送带相对滑动的路程为:△x=v•
-v μg
=v2 2μg
=v2 2μg
,x2 2μgT2
则摩擦产生的热量为:Q=μmg△x=
.故C错误.mx2 2T2
D、根据能量守恒得,传送带因传送一个工件多消耗的能量E=
mv2+μmg△x=1 2
,在时间t内,传送工件的个数n=mx2 T2
,则多消耗的能量E′=nE=t T
.故D正确.mtx2 T3
故选:AD.
