如图所示，质量为M的光滑长木板静止在光滑水平地面上，左端固定

问题问答题

如图所示，质量为M的光滑长木板静止在光滑水平地面上，左端固定一劲度系数为k的水平轻质弹簧，右侧用一不可伸长的细绳连接于竖直墙上，细绳所能承受的最大拉力为F_T，使一质量为m、初速度为v₀的小物体，在木板上无摩擦地向左滑动而后压缩弹簧，细绳被拉断，不计细绳被拉断时的能量损失．弹簧的弹性势能表达式为E_p=

kx²（k为弹簧的劲度系数，x为弹簧的形变量）．

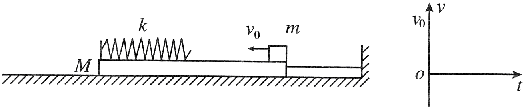
（1）要使细绳被拉断，v_o应满足怎样的条件？

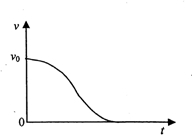
（2）若小物体最后离开长木板时相对地面速度恰好为零，请在坐标系中定性画出从小物体接触弹簧到与弹簧分离的过程小物体的v-t图象；

（3）若长木板在细绳拉断后被加速的过程中，所能获得的最大加速度为a_M，求此时小物体的速度．

答案

（1）设细绳刚被拉断时弹簧的压缩量为x₁，此时有 kx₁=F_T

为使弹簧压缩达到x₁，对小物块要求是

＞

，由此得到，细绳被拉断的条件是：v₀＞

；

（2）图象如图；

（3）当弹簧压缩至最短时，滑块有向左的最大加速度a_m，此时，设弹簧压缩量为x₂，小物体和滑块具有相同的速度v；

根据牛顿第二定律，有

kx₂=Ma_M

从小物体接触弹簧到压缩到最短，小物体、滑块和弹簧组成的系统机械能守恒，有

(M+m)v2=

解得

-(MaM)2

k(M+m)

答：（1）要使细绳被拉断，v_o应满足的条件是v₀＞

；

（2）图象如上图所示；

（3）若长木板在细绳拉断后被加速的过程中，所能获得的最大加速度为a_M，此时小物体的速度为v=

-(MaM)2

k(M+m)

．