如图所示,半径为2R的
圆弧光滑轨道AB和半径为R的1 4
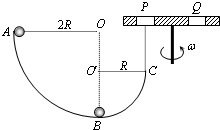
圆弧粗糙轨道BC相切于B点,两轨道置于竖直平面内,O、O′分别为两圆孤的圆心,O、O′、B三点在一条竖直线上,在C点的上方紧靠C点处有一厚度不计的水平旋转平台,平台转动角速度为,沿平台的一条直径上开有两个小孔P、Q,两孔离轴心距离相等,旋转时两孔均能到达C点正上方,一质量为m的小球自A点由静止开始下滑,滑过C点后恰能无碰撞的穿过小孔P,后又恰好无碰撞的穿过小孔Q后落入轨道中,不计空气阻力.求:1 4
(1)小球第一次滑过B点前、后瞬时对轨道的压力大小;
(2)小球第一次滑过C点时的速度大小;
(3)小球第一次经过BC段的过程中克服摩擦力所做的功.
(1)小球从A点处滑至B点时速度为vB,由动能定理得:
mg•2R=
mvB2,1 2
小球从A点处滑至B点前瞬时,对轨道的压力为N1,由牛顿第二定律得:
N1-mg=mv 2B 2R
小球从A点处滑至B点后瞬时,对轨道的压力为N2,由牛顿第二定律得:
N2-mg=mv 2B R
解得:N1=3mg,N2=5mg
(2)小球从C点处滑出后,先做匀减速上升,后自由落体,根据题意得小球在空中的运动时间
t=
(n=0,1,2,3…)(2n+1)π ω
小球第一次向上滑过C点时的速度vC=
,gt 2
vC=
,(n=0,1,2,3…)g(2n+1)π 2ω
(3)小球从A至C的过程中,小球克服摩擦力做功为W,由动能定理得:
mgR-W═
mvC2 1 2
解得:W=mgR-
,(n=0,1,2,3…)mg2π2(2n+1)2 8ω2
答:(1)小球第一次滑过B点前、后瞬时对轨道的压力大小分别是3mg,5mg;
(2)小球第一次滑过C点时的速度大小是
,(n=0,1,2,3…);g(2n+1)π 2ω
(3)小球第一次经过BC段的过程中克服摩擦力所做的功是mgR-
,(n=0,1,2,3…).mg2π2(2n+1)2 8ω2
