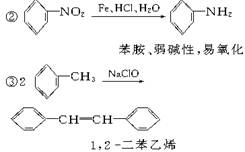
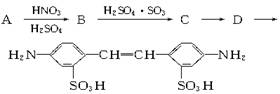
问题
填空题
函数f(x)=cos(2x-
|
答案
函数f(x)=cos(2x-
)+2sin(x-π 3
)sin(x+π 4
)π 4
=
sin2x+1 2
sin2x+(sinx-cosx)(sinx+cosx)3 2
=
cos2x+1 2
sin2x+sin2x-cos2x3 2
=
cos2x+1 2
sin2x-cos2x3 2
=sin(2x-
),π 6
∵x∈[-
,π 12
],∴2x-π 2
∈[-π 6
,π 3
],5π 6
因为f(x)=sin(2x-
)在区间[-π 6
,π 12
]上单调递增.π 3
在区间[
,π 3
]单调递减,所以当x=π 2
,f(x)取最大值l.π 3
又∵f(-
)=-π 12
<f(3 2
)=π 2
,1 2
当x=-
时,f(x)取最小值-π 12
,3 2
所以函数f(x)在区间上的值域为[-
,1].3 2
故答案为:[-
,1]3 2