问题
问答题
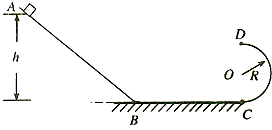
在竖直平面内,由光滑斜面和光滑半圆形轨道分别与粗糙水平面相切连接而成的轨道如图所示,半圆形轨道的半径为R=0.4m,质量为m=0.8kg可视为质点的小物块从斜面上距水平面高为h处的A点由静止开始下滑,物块通过轨道连接处的B、C点时,无机械能损失.运动到圆轨道最低点C处时对轨道的压力为N=40N,水平轨道BC长L=0.9m,滑块与水平面间的动摩擦因数为(μ=0.5,g取10m/s2.求:
(1)A点距水平面的高度h;
(2)小物块第一次由B点到C点运动的时间;
(3)小物块能否通过圆形轨道的最高点D.
答案
(1)物块通过圆形轨道最低点C时,
由牛顿第二定律得:F-mg=m
,vc2 R
由牛顿第三定律得F=N=40N,
对A到C过程,由动能定理得:
mgh-μmgL=
mvc2-0,1 2
解得:h=1.25m;
(2)物块从A点运动到B点得过程中,
由动能定理得:mgh=
mvB2,1 2
物块从B至C做匀减速直线运动,
由速度公式得:vC=vB-μgt,
解得:t=0.2s;
(3)若物块能从C点运动到D点,
由动能定理得:-mg•2R=
mvD2-1 2
mvC2,1 2
物块通过圆形轨道的最高点的最小速度为vD1,
由牛顿第二定律得:mg=m
,v2D1 R
解得:vD<vD1,
可知物块不能通过圆形轨道的最高点.
答:(1)A点距水平面的高度1.25m;
(2)小物块第一次由B点到C点运动的时间为0.2s;
(3)小物块不能通过圆形轨道的最高点D.

