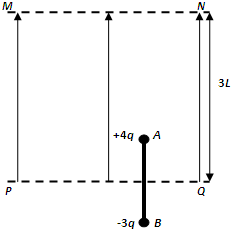
如图所示，在真空中的竖直平面内，用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B，A球的电荷量为+4q，B球的电荷量为-3q，组成一带电系统．虚线MN与PQ平行且相距3L，开始时PQ恰为杆的中垂线．在MN与PQ间加竖直向上的匀强电场，恰能使带电系统静止不动．现使电场强度突然加倍（已知当地重力加速度为g），求：
（1）B球刚进入电场时的速度v1的大小；
（2）B球的最大位移及从开始静止到最大位移处B球电势能的变化量；
（3）带电系统运动的周期T．
（1）设带电系统静止时电场强度为E，则有2mg=4qE，解得E=
①
电场强度加倍后，系统从开始静止到B进入电场，根据动能定理有
(2E×4q-2mg)L=
×2m
②
联立①②得B球刚进入电场时的速度v1=
（2）设B球在电场中的最大位移为s，经分析知A球向上越过了MN，
根据动能定理得
对整个过程：2E•4q•2L-2E•3q•s-2mg（s+L）=0
解得s=1.2L
故B球的最大位移s总=2.2L
电场力对B球做功W=-2E•3q•1.2L=-3.6mgL
所以B球电势能增加3.6mgL
（3）带电系统向上运动分为三阶段：
第一阶段匀加速运动，根据牛顿第二定律有
a1=
=g，运动时间
t1==；
第二阶段匀减速运动，同理可得a2=
=
设A球出电场时速度为v2，根据运动学公式有：v22-v12=-2a2L，
解得v2=
，
t2==2(-1)；
第三阶段匀减速运动，a3=
=
，
t3==则运动周期T=2(t1+t2+t3)=(6
-
)
答：（1）B球刚进入电场时的速度v1的大小为
；
（2）B球的最大位移为2.2L，从开始静止到最大位移处B球电势能增加3.6mgL；
（3）带电系统运动的周期T=2(t1+t2+t3)=(6
-
)
．
