在数学活动课上,同学们用一根长为1米的细绳围矩形
小题1:小明围出了一个面积为600㎝2的矩形,请你算一算,她围成的矩形的长和宽各是多少?
小题2:小颖想用这根细绳围成一个面积尽可能大的矩形,请你用所学过的知识帮他分析应该怎么围,并求出最大面积.
小题1:设她围成的矩形的一边长为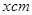 ,
,
得: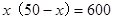 ………………(2分),
………………(2分),
 ,
,
当x=20时, ㎝;当x=30时,
㎝;当x=30时,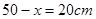 ,……………(4分)
,……………(4分)
所以小芳围成的矩形的两邻边分别是20㎝,30㎝ ……………… (5分)
小题2:设围成矩形的一边长为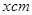 ,面积为
,面积为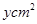 ,则有:
,则有: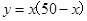 ,即
,即 ,
, 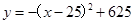 …… ………… (7分 )
…… ………… (7分 )
当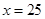 时,y最大值=625;此时,
时,y最大值=625;此时,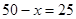 ,矩形成为正方形。即用这根细绳围成一个边长为25㎝的正方形时,其面积最大,最大面积是625
,矩形成为正方形。即用这根细绳围成一个边长为25㎝的正方形时,其面积最大,最大面积是625
分析:(1)已知细绳长是1米,则已知围成的矩形的周长是1米,设她围成的矩形的一边长为xcm,则相邻的边长是50-xcm.根据矩形的面积公式,即可列出方程,求解;
(2)设围成矩形的一边长为xcm,面积为ycm2,根据矩形面积公式就可以表示成边长x的函数,根据函数的性质即可求解.
解答:解:(1)设她围成的矩形的一边长为xcm,
得:x(50-x)=600(2分),
解得x1=20,x2=30,
当x=20时,50-x=30cm;
当x=30时,50-x=20cm,(4分)
所以小芳围成的矩形的两邻边分别是20cm,30cm(5分)
(2)设围成矩形的一边长为xcm,面积为ycm2,
则有:y=x(50-x),
即y=-x2+50x,y=-(x-25)2+625(8分)
当x=25时,y最大值=625;
此时,50-x=25,矩形成为正方形.
即用这根细绳围成一个边长为25cm的正方形时,其面积最大,最大面积是625cm2(10分)
点评:本题考查的是二次函数在实际生活中的应用,比较简单.并且通过本题要理解,最值问题的解决方法一般是转化为函数问题.
