如图,A,B是体积相同的气缸,B内有一导热的、可在气缸内无摩擦滑动的、体积不计的活塞C,D为不导热的阀门。起初,阀门关闭,A内装有压强p1=2.0×105a温度T1=300K的氮气。B内装有压强P2=1.0×105Pa,温度T2=600K的氧气。打开阀门D,活塞C向右移动,最后达到平衡,以V1和V2分别表示平衡后氮气和氧气的体积,则V1∶V2=______(假定氧气和氮气均为理想气体,并与外界无热交换,连接气缸的管道体积可忽略)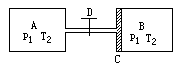
4∶1
【错解分析】错解:开始是平衡状态,未态还是平衡状态,由理想气体状态方程可知:
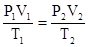 .
.
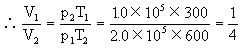
此题答案为1∶4。
理想气体状态方程或气体定律,针对的对象应为一定质量的理想气体,而不能是两种(或两部分)气体各自的状态,必须是一定质量的理想气体初、末两种状态之间满足的关系,上述解法把两部分气体的p1,p2,T1,T2与一定质量的气体前后两种状态的p1,p'1,T1,T'1混为一谈,以致出现完全相反的结论。
【正解】对于A容器中的氮气,其气体状态为:
p1=2.0×105pa V1=V T1=300K
P'1=P V'1=V1(题目所设) T'1=T
由气体状态方程可知:
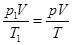 ①
①
对于B容器中的氧气,其气体状态为:
p2=1.0×105pa V2=V T2=600K
p'2=p V'2=V2(题目所设) T’2=T
由气态方程可知
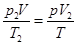 ②
②
联立①②消去T,V可得:
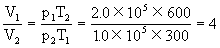
此题的正确答案为V1∶V2=4∶1
【点评】解决有关两部分气体相关联的问题时,要注意两方面的问题。首先,要把两部分气体分开看待,分别对每一部分气体分析出初、未状态的p,V,T情况,分别列出相应的方程(应用相应的定律、规律)切不可将两部分气体视为两种状态。
其次,要找出两部分气体之间的联系,如总体积不变,平衡时压强相等,等等。例如本题中,阀门关闭时两边气体体积相等,阀门打开两边气体压强相等,温度相等,利用这些关系,可以消去方程中的未知因素,否则,也解不出正确结果。
