问题
问答题
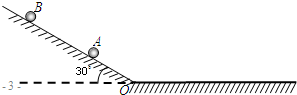
如图所示，光滑斜面倾角为30°，水平面粗糙，现将A、B两球（可视为质点）同时由静止释放，A、B两球初始位置距斜面底端O的距离分别为LA=10m、LB=40m．不考虑两球在转折O处的能量损失．重力加速度g取10m/s2则：
（1）A、B两球滑上水平面的时间差是多少？
（2）若A、B两小球与水平面间的动摩擦因数分别为μA=0.1、μB=0.5，
当B球滑上水平面后能否追上A球？若能，所用的时间是多少？若不能，A、B两小球在水平面上运动时的最短距离是多少？
答案
（1）根据牛顿第二定律得，小球在斜面上下滑的加速度为：
a=
=gsin30°=5m/s2，mgsin30° m
根据LA=
atA2得：tA=1 2
=2LA a
s=2s，2×10 5
根据LB=
atB2得：tB=1 2
=2LB a
s=4s，2×40 5
则有：△tAB=tB-tA=4-2=2s，
A、B两球滑上水平面的时间差是2s．
（2）滑上水平面A的速度为：vA=atA=5×2=10m/s，加速度大小aA=μAg=0.1×10=1m/s2，
B的速度vB=atB=5×4=20m/s，加速度大小aB=μBg=0.5×10m/s2=5m/s2，
设B滑入水平面t后与A的速度相等，
此时A在水平面上运动的时间为t+2，
则20-5t=10-（t-2）
解得t=3s，
A在t=5s时水平面上运行的位移xA=vA×5-
μAg×52=10×5-1 2
×1×25=37.5m，1 2
B在t=3s内在水平面上运动的位移xB=vBt-
μBgt2=20×3-1 2
×5×9=37.5m．1 2
由于xA=xB，所以当B球滑上水平面后恰能追上A球，所用时间为t=3s
答：（1）A、B两球滑上水平面的时间差是2s；
（2）当B球滑上水平面后能追上A球，所用的时间是3s．
和
，则下列有关说法正确的是（ ）
杂化